なぜ木は直角に枝分かれするのか、あるいは森林の炭素固定量を把握する方法
ダヴィンチはすべての枝の断面積の合計は、枝分かれする前の幹の断面積に等しいことに気づいた。

木が2本に枝分かれする場合には、
\[\pi a^2=\pi b^2 + \pi c^2\]より、
\[a^2=b^2 + c^2\]なので、直角に枝分かれすることになる。
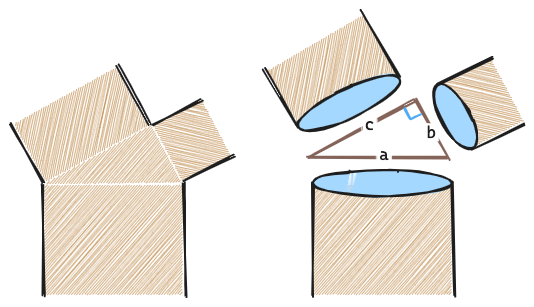
この法則はダ・ヴィンチの法則と呼ばれ現代においても概ね受け入れられているが、これに生理学的なメカニズムを基礎づけたのがパイプモデル理論である。
パイプモデル理論
まず、幹・枝は道管を通して葉に水を供給し、逆に師管を通して葉からの栄養分を運搬している。
もし、全ての葉が等しいとすれば、葉が必要とする水量と葉が生産する栄養分量は、葉の量に比例する。 そして、幹・枝が通せる水量・栄養分量も、枝の断面積に比例する。 それゆえ、枝の断面積$C$と葉量$F$は比例関係にある。
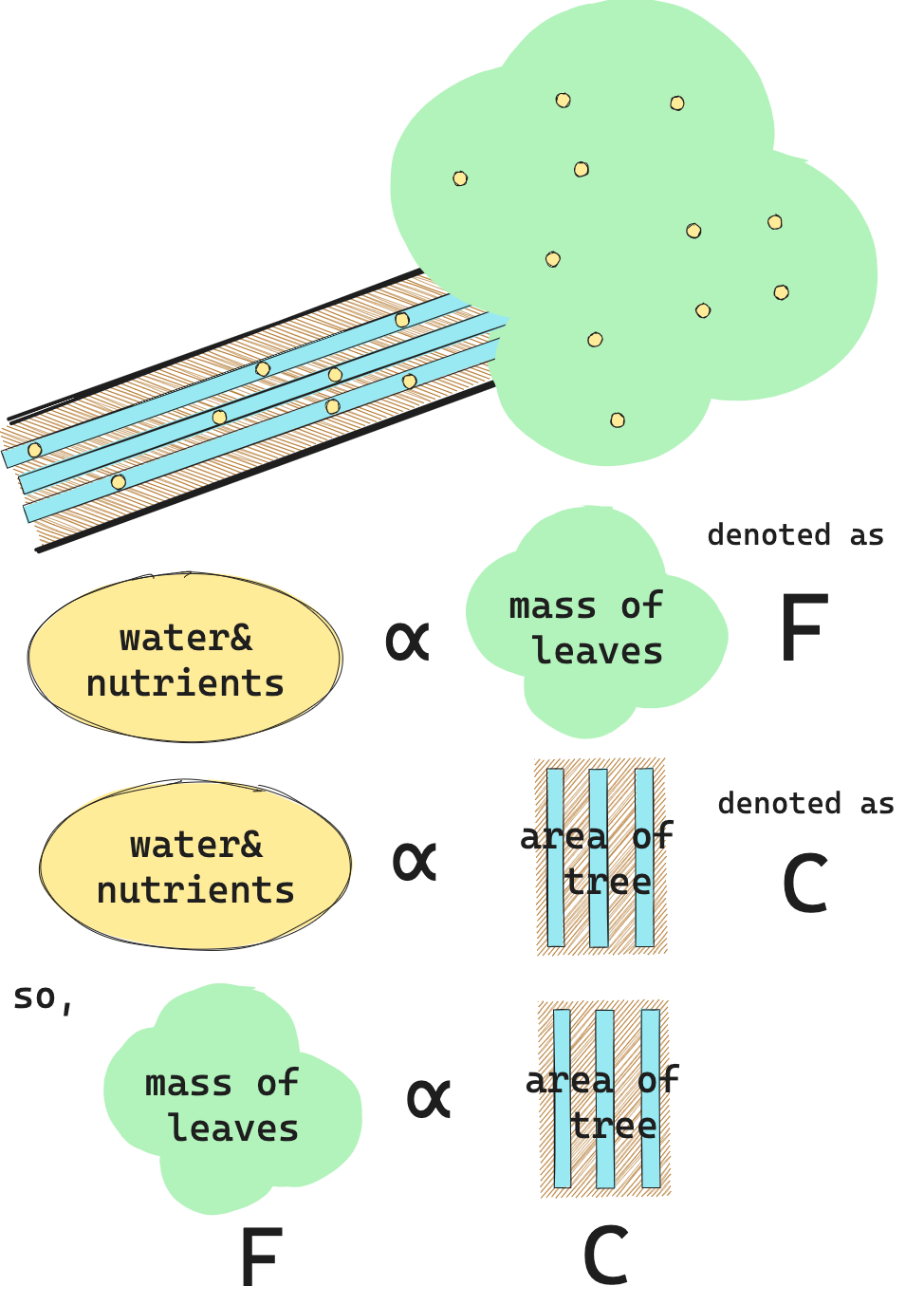
つまり、比例定数を$L$として、
\[F=LC \tag{1}\]枝分かれするときには、(枝分かれ前の幹・枝についている葉量)= (枝分かれ後のそれぞれの幹・枝についている葉量の和) が成り立つ。つまり
\[F_{total} = Σ F_i\]が成り立つ。(1)よりこれは
\[kC_{total} = Σ LC_i\]と書き換えられるので
\[C_{total} = Σ C_i\]これはダ・ヴィンチの法則そのもの、つまり(枝分かれ前の幹・枝の断面積) = (枝分かれ後のそれぞれの幹・枝の断面積の和) を表している。
So what ?
森林樹木の葉量(葉の総面積や総重量)を知ることは、森林による $CO_2$ 吸収量や、森林~大気間の水や熱の交換などを評価するうえで非常に重要とされる。そのために航空機や衛星による観測も使われるが、これらは上空からの画像しか提供できない。森林の葉量は垂直的に異なる階層(樹冠、下層木、草木層)に分布しており、上空から見えるのは主に樹冠層の葉だけなので、下層にある葉の情報を得るのは困難だ。
もちろん、樹冠層と総葉量には相関があるはずなので、その相関を得ることができれば良いのだが、そのためには、総葉量のデータを何らかの手段で得る必要がある。そこで、森林で樹木を切り倒して樹木の葉量を実際に測ることになる。とはいえ、森林全部の樹木を切り倒すわけにはいかない。
そこで、木を着倒さなくても葉量を測定できる手段が求められる。それを可能にするのがパイプモデルなのだ。つまり、(1)式
\[F=LC \tag{1}\]の$Lの値さえ分かれば、 幹の断面積$C$を求めることで(これはメジャーなどで幹の周経を測れば容易に求まる)、葉量$F$を測定することができる。
パイプモデル理論を提唱した原論文によれば、
To a more reasonable way of biomass estimation, exact knowledge on the form of tree in terms of quantitative correlations may be a prerequisite. If the form of a tree was successfully described by quantitative terms, it might possibly afford a sound basis for estimating its biomass with least error. As shown by the attempt given in the present paper, this line of approach seems fairly promising.
(日本語訳)
バイオマスの推定をよりよく行うためには、樹木の形態に関する定量的な関係を知る必要がある。もし樹木の形態が定量的な用語でうまく記述されれば、そのバイオマスを最小の誤差で推定するための確かな基盤が得られる可能性がある。本論文で示すように、このアプローチはかなり有望であるように思われる。
そして、実際にいくつかの樹木を切り倒して$F$(論文では$F(z)$)と$C$(論文では$C(z)$)の関係について調べ、比例関係にあることを示し、
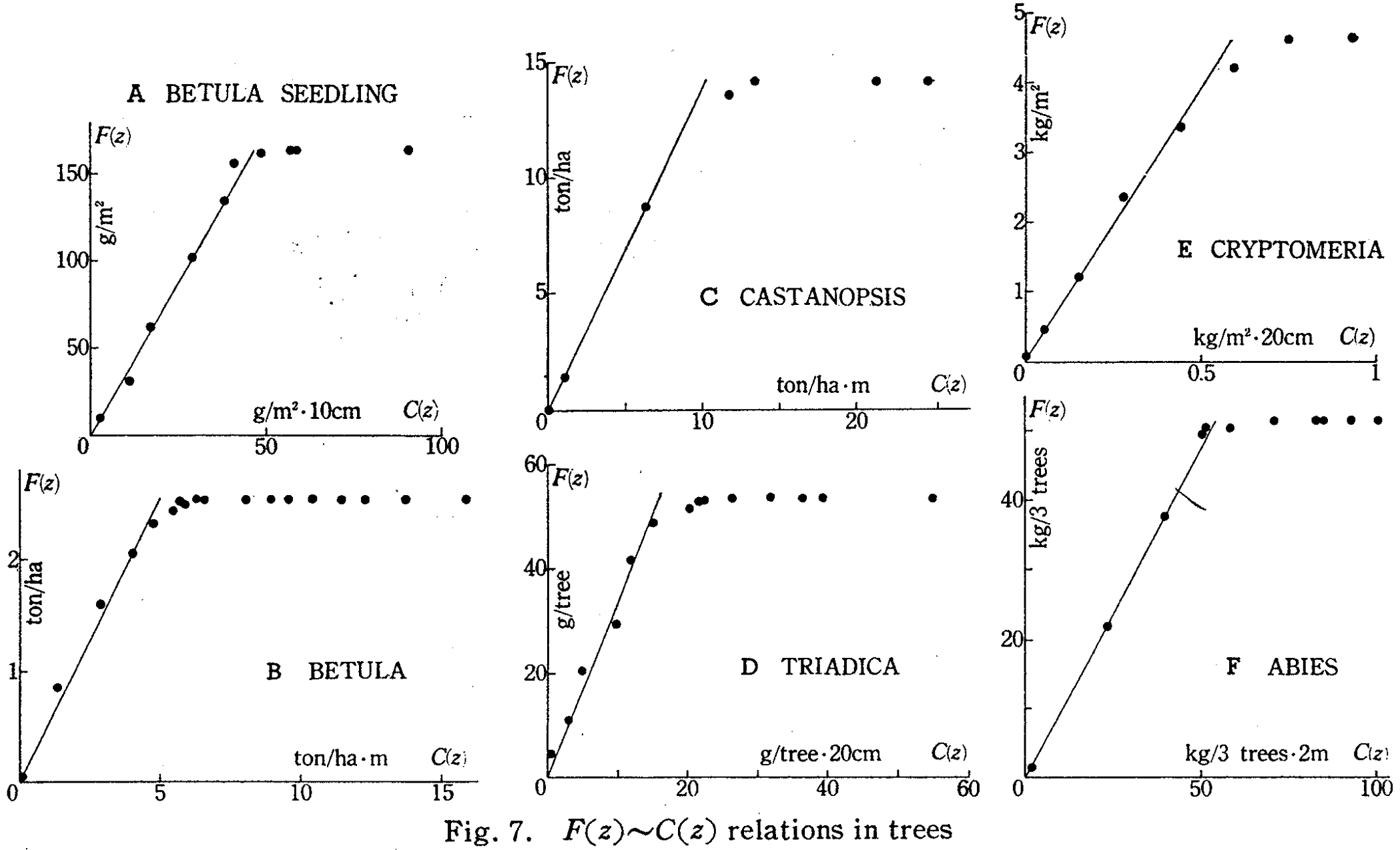
この論文では続けて、いくつかの種の木について実際にLを求め、$L$の大きさは厳密には種に固有ではなく葉量の増減に応じて季節的にも変化し、また個体密度にも依存することを示している。
このことは種ごとに異なる$L$を当てはめる必要があるだけでなく、季節や個体密度などの様々な要因を考慮にいれなければLを決定できない、つまり葉量$F$を推定できないことを示しているが、逆に$L$の値がこのように生育条件に依存することは、$L$から生育条件を推定できることも示唆しており、むしろ$L$の有用性を示すものとも考えられる。
アロメトリー
このような考え方は一般にはアロメトリーと言われる。アロメトリーとは生物の体の大きさ(体重や身長など)と、その形態や生理的機能(器官の大きさや代謝率など)との間の関係を研究する分野だ。例えば、全ての生物種で大まかには代謝量は体重の3分の4乗に比例することが知られている。
アロメトリーとはdifferent measureを意味してアイソメトリーと対義される。
生物にとってアロメトリーな成長は本質的とも言える。
生物の体を直方体でモデリングした場合、生物の体の長さの全ての部分が等しく2倍になると、表面積は4倍に増加し、その体積と質量が8倍に増加することが分かる。 これは生物に問題を引き起こす可能性がある。例えば、骨と筋肉の強度は断面積に依存しているので、脚が支える質量は8倍になったのにもかかわらず、断面積は4倍にしか増加していないことから、小さいときよりも2倍の骨と筋肉の負荷を経験することになります。同じように、代謝する組織量は8倍になるが、呼吸器の表面積は4倍にしか増加していないので、このままでは酸素を十分に受け渡すことができない。 つまり、アイソメトックなスケーリングでは、身体的要求との間に不一致が生じる。この不一致は組織の成長率を比率を変更すること(=different measure アロメトリー)で回避できる。
この論文はどのように発展するか?
Fig.7で、$C$に対して$F$が比例関係になっていない領域があるが、これは、古い葉が枯れ落ち、古いパイプが封入される幹の根元付近では、それより先についている葉量$F$が一定でも、幹の断面積$C$が小さくなっている部分があることによる。(枯れ落ちた葉は白丸で表され、生きている葉は黒丸で表されている。)
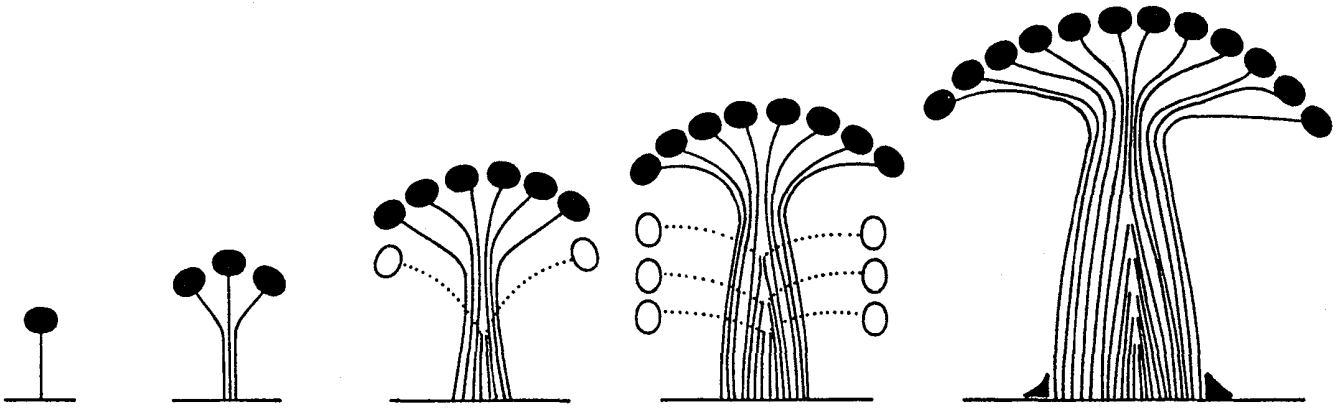
これは、比例定数$L$が正確に分かっても、実際には木の根元ではなく、生きた枝が最初に分岐する高さ(“生枝下高”と言われる)の幹の断面積を測る必要があることを意味する。根本であれば容易に測れるが、生枝下高の幹の太さを測るには木登りしなくてはいけない。これは大変ということで、次に考えるは木の根元の断面積と生枝下高の断面積のアロメトリーである。
実際、両者にも一定の関係があることが調べられている。
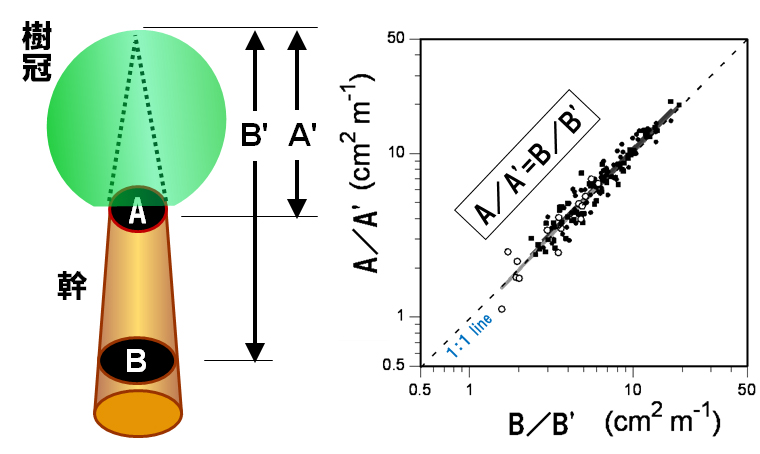
詳しくは最近の研究トピック(2)-その1 隅田研究室を参照
参考文献
植物形のパイプ ・モデル理論とその展開 京大 ・農 大畠 誠一 生物の体サイズとアロメトリー:エネルギー代謝量と体サイズ 八 木 光 晴・及 川 信